Page 62 - MATINF Nr. 6

˘
62 PROBLEME DE MATEMATICA PENTRU EXAMENE

Teste gril˘a pentru admiterea la facultate

TESTUL 1

Mihaela Gabor 1

√ p √
1. Fie funct¸ia f : [1, ∞) → R, f(x) = x − 1+ x + 24 − 10 x − 1. Intervalul maxim pentru
care funct¸ia este constant˘a este:
a) [1, ∞); b) [2,3]; c) [1,26]; d) [24,26]; e) Ø;

1
2
2. Valoarea lui x pentru care are loc egalitatea C + C + ... + C x x−1 = 254 este:
x
x
a) x = 10; b) x = −10; c)x = 8; d) x = 100; e) x = 54;
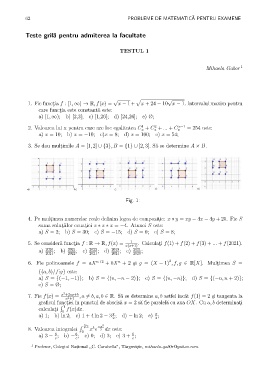
3. Se dau mult , imile A = [1, 2] ∪ {3}, B = {1} ∪ [2, 3]. S˘a se determine A × B.

Fig. 1:

4. Pe mult¸imea numerelor reale definim legea de compozit¸ie: x ∗ y = xy − 4x − 4y + 20. Fie S
suma solut¸iilor ecuat¸iei x ∗ x ∗ x = −4. Atunci S este:
a) S = 2; b) S = 30; c) S = −15; d) S = 0; e) S = 8;

5. Se consider˘a funct¸ia f : R → R, f(x) = 1 . Calculat¸i f(1) + f(2) + f(3) + ... + f(2021).
x(x+1)
a) 2020 ; b) 2021 ; c) 2022 ; d) 2019 ; e) 2021 ;
2021 2022 2021 2021 2020
2
n
6. Fie polinoamele f = aX n+2 + bX + 2 ¸si g = (X − 1) , f, g ∈ R[X]. Mult¸imea S =
.
.
{(a, b)/f.g} este:
a) S = {(−1, −1)}; b) S = {(n, −n − 2)}; c) S = {(n, −n)}; d) S = {(−n, n + 2)};
e) S = Ø;
2
7. Fie f(x) = x +2ax+b , a 6= b, a, b ∈ R. S˘a se determine a, b astfel ˆıncˆat f(1) = 2 ¸si tangenta la
2
x +1
graficul funct¸iei ˆın punctul de abscis˘a x = 2 s˘a fie paralel˘a cu axa OX. Cu a, b determinat¸i
R 1
calculat¸i f(x)dx.
0
π
π
a) 1; b) ln 2; c) 1 + 4 ln 2 − 3 ; d) − ln 2; e) ;
2 2
√
R 3 3 −x 3
5
8. Valoarea integralei 0 x e 3 dx este:
6
6
6
a) 3 − ; b) − ; c) 0; d) 3; e) 3 + ;
e e e
1
Profesor, Colegiul Nat , ional ,,C. Carabella”, Tˆargovi¸ste, mihaela gab0r@yahoo.com