Page 54 - MATINF Nr. 8

˘
54 PROBLEME DE MATEMATICA PENTRU EXAMENE

2
a) Demonstrat , i c˘a: 2x − 5x − 25 = (2x + 5) · (x − 5), ∀x ∈ R.
b) Ar˘atat , i c˘a: E (x) = 1, ∀x ∈ R.
3. Fie funct , ia f : R → R, f (x) = x + 4.
a) Aflat , i coordonatele punctului M, unde M este piciorul perpedicularei duse din O la
graficul funct , iei f.
a
b) Determinat , i a s , i b, s , tiind c˘ punctul T (a, b) ∈ G f s , iˆındeplines , te condit , ia: f (a + b) =
2 · f (3a + 2b) .
ˆ
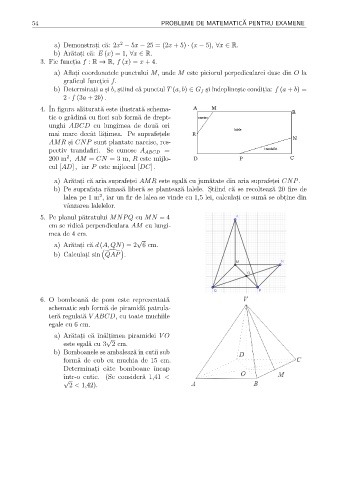
4. In figura al˘aturat˘a este ilustrat˘a schema-
tic o gr˘adin˘a cu flori sub form˘a de drept-
unghi ABCD cu lungimea de dou˘a ori
mai mare decˆat l˘at , imea. Pe suprafet , ele
AMR s , i CNP sunt plantate narcise, res-
pectiv trandafiri. Se cunosc A ABCD =
2
200 m , AM = CN = 3 m, R este mijlo-
cul [AD] , iar P este mijlocul [DC] .

a) Ar˘atat , i c˘a aria suprafet , ei AMR este egal˘a cu jum˘atate din aria suprafet , ei CNP.
b) Pe suprafat , a r˘amas˘a liber˘a se planteaz˘a lalele. S , tiind c˘a se recolteaz˘a 20 fire de
2
lalea pe 1 m , iar un fir de lalea se vinde cu 1,5 lei, calculat , i ce sum˘a se obt , ine din
vˆanzarea lalelelor.

5. Pe planul p˘atratului MNPQ cu MN = 4
cm se ridic˘ perpendiculara AM cu lungi-
a
mea de 4 cm.
√
a) Ar˘atat , i c˘a d (A, QN) = 2 6 cm.
Ä ä
b) Calculat , i sin QAP .
’

6. O bomboan˘a de pom este reprezentat˘a
a
schematic sub form˘ de piramid˘ patrula-
a
ter˘a regulat˘a V ABCD, cu toate muchiile
egale cu 6 cm.
a) Ar˘atat , i c˘a ˆın˘alt , imea piramidei V O
√
este egal˘a cu 3 2 cm.
b) Bomboanele se ambaleaz˘ˆın cutii sub
a
form˘a de cub cu muchia de 15 cm.
ı
Determinat , i cˆate bomboane ˆncap
ˆıntr-o cutie. (Se consider˘a 1,41 <
√
2 < 1,42).