Page 50 - MATINF Nr.2

50 L. Deaconu

Construim cele 3 mediane (alegem
”Segment ˆıntre dou˘a puncte” s , i se-
lect˘am succesiv punctele A, D, B,
E, C, F) s , i not˘am centrul de gre-
utate al triunghiului ABC (alegem
”Intersect , ie dou˘a obiecte” s , i select˘am
dou˘a mediane, de exemplu AD s , i
BE). Not˘am punctul obt , inut cu G
(fig. 16).

Figura 16.

Pentru a sugera c˘a punctele H, G
s , i O sunt coliniare m˘asur˘am unghiul
HGO. Alegem ”Unghi” s , i select˘am
÷
punctele H, G s , i O, ˆın aceast˘a ordine.
Observ˘am c˘a unghiul are m˘asura de
◦
180 (fig. 17). Dreapta pe care se afl˘a
cele trei puncte se numes , te Dreapta
lui Euler (a triunghiului ABC).

Figura 17.

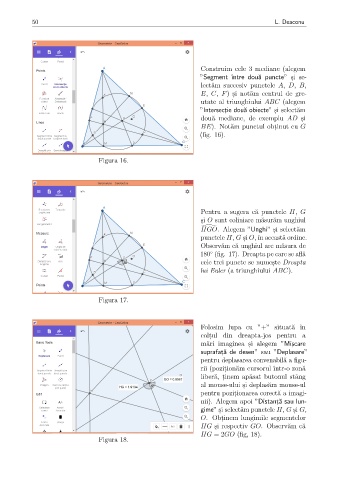
Folosim lupa cu ”+” situat˘a ˆın
colt , ul din dreapta-jos pentru a
m˘ari imaginea s , i alegem ”Mis , care
suprafat ,˘a de desen” sau ”Deplasare”
pentru deplasarea convenabil˘a a figu-
rii (pozit , ion˘am cursorul ˆıntr-o zon˘a
liber˘a, t , inem ap˘asat butonul stˆang
al mouse-ului s , i deplas˘am mouse-ul
pentru pozit , ionarea corect˘a a imagi-
nii). Alegem apoi ”Distant ,˘a sau lun-
gime” s , i select˘am punctele H, G s , i G,
O. Obt , inem lungimile segmentelor
HG s , i respectiv GO. Observ˘am c˘a
HG = 2GO (fig, 18).
Figura 18.