Page 25 - MATINF Nr.2

A dynamic identity in a triangle and some applications

Thanos Kalogerakis 1

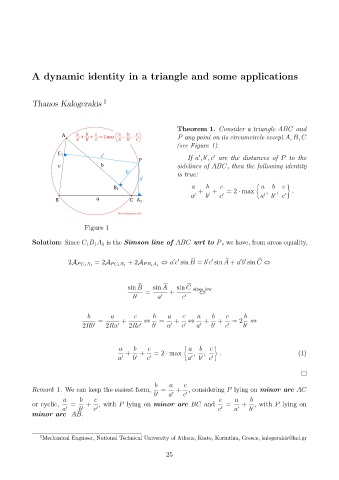
Theorem 1. Consider a triangle ABC and
P any point on its circumcircle except A, B, C
(see Figure 1).

0
0
0
If a , b , c are the distances of P to the
sidelines of ABC, then the following identity
is true:
a b c ® a b c ´
+ + = 2 · max , , .
a 0 b 0 c 0 a 0 b 0 c 0

Figure 1

Solution: Since C 1 B 1 A 1 is the Simson line of ABC wrt to P, we have, from areas equality,

0 0
0 0
0 0
⇔ a c sin B = b c sin A + a b sin C ⇔
“
“
“
2A PC 1 A 1 = 2A PC 1 B 1 + 2A PB 1 A 1
sin B sin A sin C sines low
“
“
“
= + ⇔
b 0 a 0 c 0
b a c b a c a b c b
= + ⇔ = + ⇔ + + = 2 ⇔
2Rb 0 2Ra 0 2Rc 0 b 0 a 0 c 0 a 0 b 0 c 0 b 0

a b c ® a b c ´
+ + = 2 · max , , . (1)
a 0 b 0 c 0 a 0 b 0 c 0

b a c
Remark 1. We can keep the easiest form, = + , considering P lying on minor arc AC
b 0 a 0 c 0
a b c c a b
or cyclic, = + , with P lying on minor arc BC and = + , with P lying on
a 0 b 0 c 0 c 0 a 0 b 0
minor arc AB.

1
Mechanical Engineer, National Technical University of Athens, Kiato, Korinthia, Greece, kalogerakis@hol.gr

25